Simulation
Simulation
Groundbreaking software for simulating the performance of Markforged printed parts in Eiger™. Included in the Digital Forge Complete Advanced Plan.

Validate part performance and optimize print settings to ensure parts meet requirements while maximizing manufacturing efficiency. All at the speed of software.
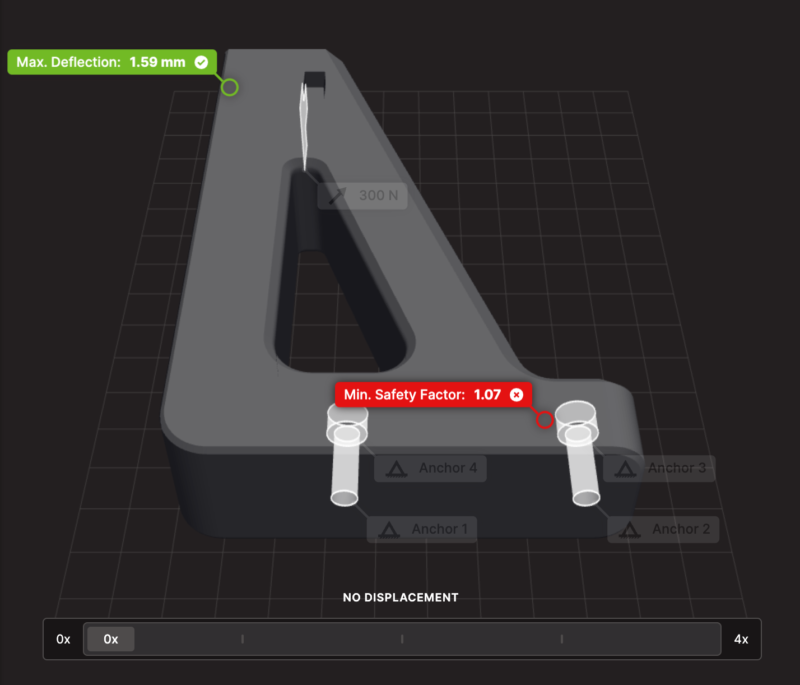
Simulate the strength and stiffness of a part printed with user defined settings.
-
Simple, intuitive feedback and a visualization of how the part deforms under loading.
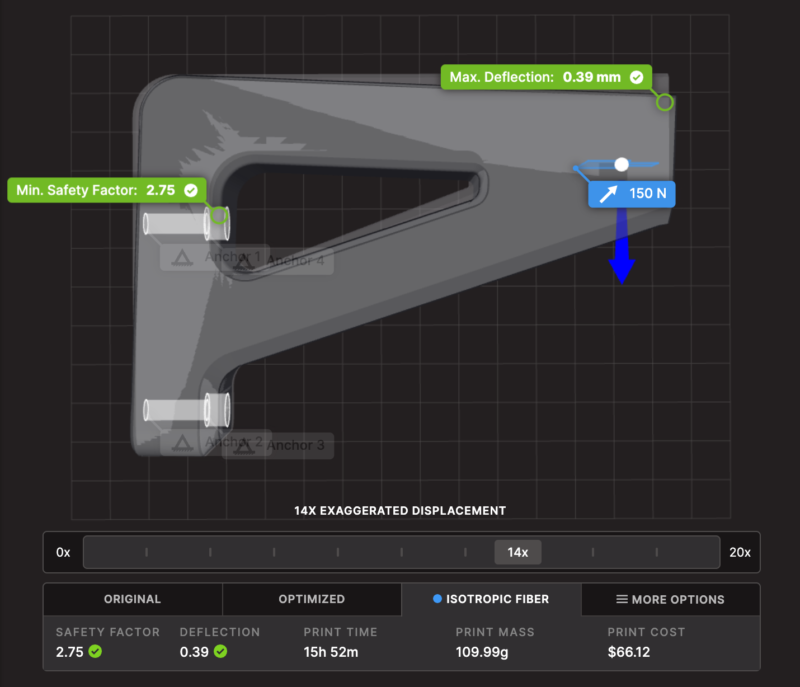
Automatically configure the print settings to satisfy performance requirements and minimize print time and material consumption.
-
Pick the best option for your needs from multiple solutions.
The Value of Simulation
Helps take the guesswork out of configuring parts
Gain confidence that parts will perform as required |
Shortens the product development timeline
Replaces costly and time consuming physical testing |
Maximizes manufacturing efficiency and minimizes costs
Unlocks additional, high-value applications |
Simulation is available in the Digital Forge Complete Advanced Plan.
Resources
-
Learn Blog Customer Success Stories

Siemens Energy Technology Application Center
Siemens Energy uses Simulation for fast and accurate structural analysis of part designs— allowing fast print times for structurally sound parts. -
Learn Blog Customer Success Stories

PUNCH Torino
PUNCH Torino, an R&D and engineering facility, 3D prints a camshaft locking tool with Simulation software: reducing eight design iterations to just one.
Let’s get started.